Blogia
355ml

Multiplicación de una matriz por un escalar

Multiplicación de una matriz por un escalar 

Dada una matriz A de m filas y n columnas, lo que podemos denotar como:

A:=(a_{ij})_{m times n}

la multiplicación de A por un escalar k, que se denota k·A, k×A o simplemente kA, está definida como:

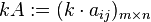
kA:=(kcdot a_{ij})_{m times n}

es decir, corresponde a la matriz conformada por cada elemento de la matriz multiplicado por dicho escalar.

Gráficamente, si 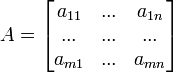A = begin{bma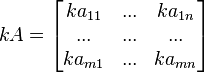trix} a_{11} & ... & a_{1n} ... & ... & ... a_{m1} & ... & a_{mn} end{bmatrix}    y     kinmathbb{R},    entonces     kA = begin{bmatrix} ka_{11} & ... & ka_{1n} ... & ... & ... ka_{m1} & ... & ka_{mn} end{bmatrix}

La multiplicación por escalar es análoga a la suma o resta de matrices, y cumple con las mismas características de la multiplicación aritmética. En efecto, podemos llegar al mismo resultado sumando k veces la misma matriz A entre sí.

Multiplicación de una matriz por una matriz 

Los resultados en las posiciones marcadas dependen de las filas y columnas de sus respectivos colores.

Dadas dos matrices A y B, tales que el número de columnas de la matriz A es igual al número de filas de la matriz B; es decir:

A:=(a_{ij})_{m times n} y B:=(b_{ij})_{n times p}

la multiplicación de A por B, que se denota A·B, A×B o simplemente AB, está definida como:

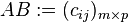
AB:=(c_{ij})_{m times p}

donde cada elemento ci,j está definido por:

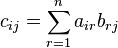
c_{ij} = sum_{r=1}^n a_{ir}b_{rj}

Gráficamente, si 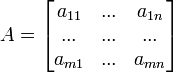A = begin{bmatrix} a_{11} & ... & a_{1n} ... & ... & ... a_{m1} & ... & a_{mn} end{bmatrix}    y     B = begin{bmatrix} b_{11} & ... & b_{1p} ... & ... & ... b_{n1} & ... & b_{np} end{bmatrix}
      entonces  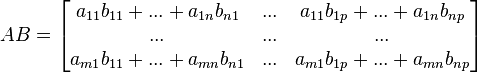AB = begin{bmatrix} a_{11}b_{11}+...+a_{1n}b_{n1} & ... & a_{11}b_{1p}+...+a_{1n}b_{np} ... & ... & ... a_{m1}b_{11}+...+a_{mn}b_{n1} & ... & a_{m1}b_{1p}+...+a_{mn}b_{np} end{bmatrix}

0 comentarios